Table of Contents
Toggleclass 10 maths 3.3 solutions
NCERT Solutions For Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
Download the free NCERT Maths Chapter 3 Solutions for Class 10 here. Pair of Linear Equations in Two Variables in Maths Class 10 NCERT Solutions are a great resource for homework assistance. For class 10 maths 3.3 solutions Expert Bhautikstudy.com Teachers developed the NCERT Solutions. Complete solutions to all the problems in NCERT Textbook’s Chapter 3 Math Class 10 Pair of Linear Equations in Two Variables Exercise 3.3.
Class 10 Maths 3.3 Solutions Question 1.
1. Solve the following pair of linear equations by the elimination method and the substitution method:
(i) x + y = 5 and 2x – 3y = 4
(ii) 3x + 4y = 10 and 2x – 2y = 2
(iii) 3x – 5y – 4 = 0 and 9x = 2y + 7
(iv) x/2+ 2y/3 = -1 and x-y/3 = 3
Solution:






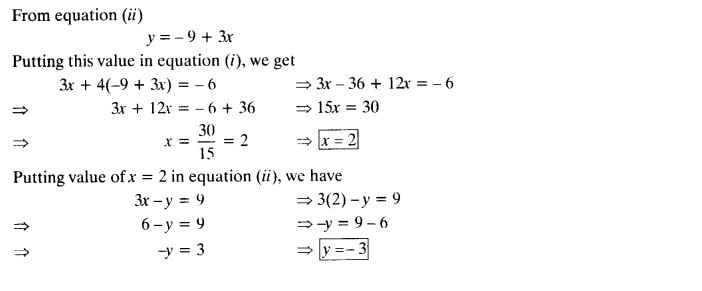
Class 10 Maths 3.3 Solutions Question 2.
2. Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method :
(i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes 1 2 if we only add 1 to the denominator. What is the fraction?
(ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
(iii) The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
(iv) Meena went to a bank to withdraw ₹2000. She asked the cashier to give her ₹50 and ₹100 notes only. Meena got 25 notes in all. Find how many notes of ₹50 and ₹100 she received.
(v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ₹ 27 for a book kept for seven days, while Susy paid ₹21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
Solution:




Maths in Class 10: Pair of Linear Equations in Two Variables
class 10 maths 3.3 solutions-
Overview
You have covered Linear Equations in Two Variables in previous sessions. It has also been studied that there are an endless number of solutions to a linear equation in two variables. This chapter will review and expand on the understanding of linear equations in two variables to include pairs of linear equations in two variables.
Two Differential Linear Equations
A linear equation in two variables, x and y, is an equation that takes the form ax + by + c = 0, where a, b, and c are real values and a and b are not zeros. A pair of values, one for x and the other for y, that equalises the two sides of the equation is the solution to such a problem. Along with appropriate examples, the topic also covers the geometrical representation of a pair of linear equations in two variables here class 10 maths 3.3 solutions play an important role.
Pair of Linear Equations in Two Variables, Class 10 Maths System of Mind Maps for Two Linear Equations in Two Variables
In class 10 maths 3.3 solutions In several disciplines, including physics, engineering, economics, and computer graphics, polynomials are widely employed.
These are basic polynomial notes appropriate for a class 10 setting. They address fundamental ideas, procedures, factorization, equations, and application domains. class 10 maths 3.3 solutions are crucial in this context.
Linear Equation Depicted in Two Variables
Each solution (x, y) to a linear equation in two variables, ax + by + c = 0, corresponds to a point on the line representing the equation, and vice versa. Every linear equation in two variables is graphically represented as a line here class 10 maths 3.3 solutions play an important role.
Procedure for Solving a Set of Two Linear Equations in Two Variables
The necessary solution is the coordinate of the point (x, y) that satisfies the system of pairwise linear equations in two variables. The intersection of the two lines that represent the two equations is at this position.
Two approaches exist for solving a set of linear equations in two variables.
(1) Visual Approach: When the point used to symbolise the answer has non-integral coordinates, this method is less practical.
(2) Algebraic Method: In cases where the point used to represent the solution has non-integral coordinates, this method is more practical.
The Substitution Method, the Elimination Method, and the Cross Multiplication Method are the three further divisions of this approach.