Units and Measurements Class 11 Notes Class 11 CBSE

Ch-1 Units and Measurements

Topic Covered

–Latest CBSE syllabus 2024-2025

-Introduction, Dimensions

-Application of Dimension Analysis – Principle of Homogeneity 

-To Derive the relation among Various Physical Quantities.

-Units, Basic Units, CGS, MKS, FPS

-Units Conversion

-Significant Figure

-All types of Numericals Based on CBSE, JEE, NEET, NDA. 

Units and measurements class 11 notes

Physical Quantities
Physical quantities are those that can be used to express the rules of physics. Any quantity that can be measured is considered physical. As a result, physical quantities include mass, time, length, pressure, temperature, current, and resistance.

Categorization of Physical Measurements

The physical quantities are divided into

(i) Base quantities or fundamental quantities

(ii) Calculated amounts

Fundamental quantities are those physical quantities that do not depend on one another. The phrase “derived quantities” refers to all additional quantities that can be stated in terms of the fundamental quantities.

Measures

The unit is the name of the reference standard that is used to measure the physical quantities.

Characteristics of the unit

1. The device needs to be a decent size.

2. The unit needs to be clearly specified.

3. The unit must not vary with location in order to be readily reproducible.

4. The unit can’t evolve over time.

5. The unit shouldn’t alter in response to external factors like pressure, temperature, etc.

6. The unit ought to be easily compared to similar physical quantities in experiments.

Unit Types

(i) Fundamental Units

Fundamental units are the units specified for the fundamental quantities.

(ii) Derived Units

The terms “derived units” refer to the units of all other physical quantities that are derived from the fundamental units.

Unit System

(1) FPS System: This system uses feet as the unit of length, pounds as the unit of mass, and seconds as the unit of time.

(2) CGS System: This system uses centimetres, grammes, and seconds as the units of length, mass, and time, respectively.

(3) MKS System: This system uses metres, kilogrammes, and seconds as the units of length, mass, and time, respectively.

(4) SI System: This system is widely applied globally in all measures. Two supplemental units and seven fundamental units form the foundation of the system.

Basic Units
Quantity	Unit	Symbol of the Unit
Length	metre	m
Mass	kilogram	kg
Time	second	s
Temperature	kelvin	K
Electric current	ampere	A
Number of particles	mole	mol
Luminous intensity	candela	cd
Supplementary Units
Plane angle	radian	rad
Solid angle	Steradian	sr

 

Basic and Supplementary Units Definition

Fundamental Units

1. Metre (m): In a vacuum, one metre is the distance that light travels in a second (1/299792458).

The mass of a platinum-iridium cylinder stored at the National Bureau of Weights and Measurements in Paris is measured in kilogrammes (kg).

3. Second (s): The second is the amount of time it takes for a caesium-133 atom’s light to travel a given wavelength and complete 9192631770 vibrations.

4. Ampere (A): In a vacuum, two straight parallel conductors of infinite length and negligible cross-section spaced one metre apart are said to produce a force between them equivalent to two x 10-7 newtons per metre of length when one ampere of current is carried through them.

5. Kelvin (K): This is the percentage 1/273.6 of the water’s triple point thermodynamic temperature.

6. Candela (cd): The unit of measurement for luminous intensity is 1/60th of a square centimetre for a perfect black body kept at platinum’s freezing point (1773 0C).

7. Mole (mole): The quantity of material with elementary units equal to the number of atoms in 0.012 kg of carbon-12 is known as a mole.

Dimensional Formula

In Units and Measurement class 11 Notes Any physical quantity can be measured using one of the fundamental units; its dimensional formula indicates which unit of measurement was employed.

For a physical quantity, how is the dimensional formula written?

(1) The physical quantity’s formula needs to be put in writing. The quantity needs to be in the equation’s left half.

(2) Every quantity on the formula’s right side needs to be expressed in terms of basic quantities like mass, length, and time.

(3) Substitute M, L, and T for mass, length, and time, respectively.

(4) Summarise the phrases’ powers.

Features of Dimensions(units and measurements class 11 notes)

(1) The dimensions are independent of the unit system.

It is possible to add or subtract quantities that have comparable dimensions from one another.

(3) The physical quantities’ units can be used to determine dimensions, and vice versa.

(4) It is possible for two distinct quantities to share a dimension.

(5) The dimension of the third quantity is formed by multiplying or dividing two dimensions.

Analysing Dimensions

Utilising the dimensional formula, one can

(1) Verify that the equation is correct.

(2) Change the physical quantity’s unit of measurement from one system to another.

(3) Determine the relationship between the physical quantities.

Units and Dimensions of a Few Derived Quantities(units and measurements class 11 notes)

Physical Quantity	Unit	Dimensional Formula
Displacement	m	M0L1T0
Area	m2	M0L2T0
Volume	m3	M0L3T0
Velocity	ms-1	M0L1T-1
Acceleration	ms-2	M0L1T-2
Density	Kg m-3	M1L-3T0
Momentum	Kg ms-1	M1L1T-1
Work/Energy/Heat	Joule (or) Kg m2/sec2	M1L2T-2
Power	Watt (W) (or) Joule/sec	M1L2T-3
Angular Velocity	rad s-1	M0L0T-1
Angular Acceleration	rad s-2	M0L0T-2
Moment of Inertia	Kg m2	M1L2T0
Force	Newton (or) Kg m/sec2	M1L1T-2
Pressure	Newton/m (or) Kg m-1/sec2	M1L-1T-2
Impulse	Newton sec (or) Kg m/sec	M1L1T-1
Inertia	Kg m2	M1L2T0
Electric Current	Ampere (or) C/sec	QT-1
Resistance/Impedance	Ohm (or) Kg m2/sec C2	ML2T-1Q-2
EMF/Voltage/Potential	Volt (or) Kg m2/sec2 C	ML2T-2Q-1
Permeability	henry/m (or) Kg m/C2	MLQ-2
Permittivity	Farad/m (or) sec2C2/Kgm3	T2Q2M-1L-3
Frequency	Hertz (or) sec-1	T-1
Wavelength	m	L1

Principle of Homogeneity(units and measurements class 11 notes)

According to the principle of homogeneity of dimensions, all the terms in a given physical equation must be the same.

Ex. s = ut + (½) at²

Dimensionally

[L] = [LT^-1.T] + [LT^-2. T²] [L] = [L] + [L]

Dimensional Analysis’s Flaws(units and measurements class 11 notes)

The proportionality constant cannot be established during formula derivation.
It is impossible to derive the equation of a physical quantity that depends on more than three distinct physical quantities.
If there are more parameters influencing the physical quantity than there are fundamental quantities, then this method cannot be applied.
It is impossible to deduce the equations comprising exponential and trigonometric functions.

Things to Bear in Mind(units and measurements class 11 notes)

-Physical quantities are those that can be used to express the rules of physics. For instance, mass, length, and time.
-There are two categories for physical quantities: derived quantities and fundamental quantities.
-The unit is the name of the reference standard that is used to measure the physical quantities. There are two categories for units: derived units and fundamental units.
-The most widely used system of units is the SI system.
-Two supplemental units and seven fundamental units form the foundation of the SI.
-Any physical quantity can be measured using one of the fundamental units; its dimensional formula indicates which unit of measurement was employed.
-The dimensional formula adheres to the homogeneity principle.

 

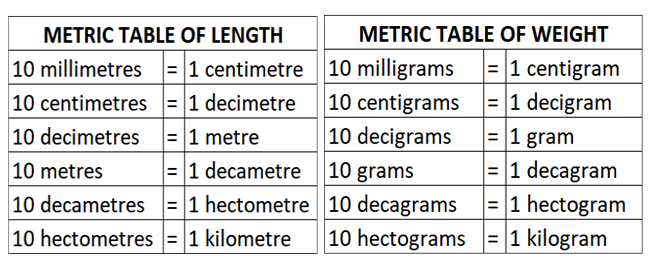
Other Important Units of Length(units and measurements class 11 notes)
For measuring large distances e.g., distances of planets and stars etc., some bigger units of length such as ‘astronomical unit’, ‘light year’, parsec’ etc. are used.
• The average separation between the Earth and the sun is called one astronomical unit.
1 AU = 1.496 x 10¹¹ m.
• The distance travelled by light in vacuum in one year is called light year.
1 light year = 9.46 x 10¹⁵ m.
• The distance at which an arc of length of one astronomical unit subtends an angle of one second at a point is called parsec.
1 parsec = 3.08 x 10¹⁶ m
• Size of a tiny nucleus = 1 fermi = If = 10^-15 m
• Size of a tiny atom = 1 angstrom = 1A = 10^-10 m

The Parallax Approach(units and measurements class 11 notes)

In units and measurements class 11 notes the distances of planets and stars from Earth are calculated using this method.
The parallax. With a pen in front of your eyes, close your right eye first, then your left, to focus on it. What have you noticed? The pen’s location varies in relation to the background. The term parallax refers to this relative change in the pen’s (or object’s) position with respect to the background.
In units and measurements class 11 notes the distance of a distant object from the basis is given by if it is a planet or star, for example, and it subtends parallax angle 0 on an arc of radius b on Earth.

Pendulum clocks, mechanical watches (in which vibrations of a balance wheel are used) and quartz watches are commonly used to measure time. Cesium atomic clocks can be used to measure time with an accuracy of 1 part in 10¹³ (or to a maximum discrepancy of 3 ps in a year).

Uses of Dimensions(units and measurements class 11 notes)
The following applications are made of the notion of dimensions and dimensional formulae:
(i) Verifying the outcomes;

(ii) Converting between different unit systems;

(iii) Determining the links between physical quantities;

(iv) Scaling and model analysis.

In units and measurements class 11 notes the homogeneity of dimensions idea serves as the foundation for many applications. This principle states that only dimensionally identical quantities may be added to or subtracted from one another, and that the “net” dimensions of the various physical quantities on both sides of an acceptable physical relation must be the same.

Dimensional Analysis’s Drawbacks(units and measurements class 11 notes)
The following are some limitations of the dimensions method:
(i) The dimensionless constant’s value cannot be determined using this method.
(ii) The equation comprising logarithmic, exponential, and trigonometric terms cannot be analysed using this method.
(iii) In mechanics, if a physical variable depends on more than three components, it is impossible to establish a relationship between them since equalising the powers of M, L, and T yields only three equations.
(iv) It is unable to determine if the quantity is scalar or vector.

The Guidelines for Calculating the Count of Significance(units and measurements class 11 notes)
(i) Every digit that is not zero is important.
(ii) Every zero in between a non-zero digit has meaning.
(iii) In integers lacking a decimal point, all zeroes to the right of the final non-zero digit are meaningless.
(iv) There is no significance to any zeroes to the left of a non-zero digit or to the right of a decimal point.
(v) Every zero that appears after a decimal point and before a non-zero digit is important.
(vi) The least decimal place among the values operated upon shall be retained in the result for addition and subtraction.