Table of Contents
ToggleClass 10 maths 9.1 NCERT solutions
NCERT Solutions For Class 10 Maths Chapter 10 Some Applications of Trigonometry Ex-9.1
Download the free NCERT Maths Chapter 9 Solutions for Class 10 here Introduction to Trigonometry in Maths Class 10 NCERT Solutions are a great resource for homework assistance. For class 9 maths 9.1 NCERT solutions Expert Bhautikstudy.com Teachers developed the NCERT Solutions. Complete solutions to all the problems in NCERT Textbook’s Chapter 8 Math Class 10 Triangles Exercise 9.1.
Class 10 Maths 9.1 NCERT Solutions Question 1.
1. A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°. (see fig. 9.11)

Solution:
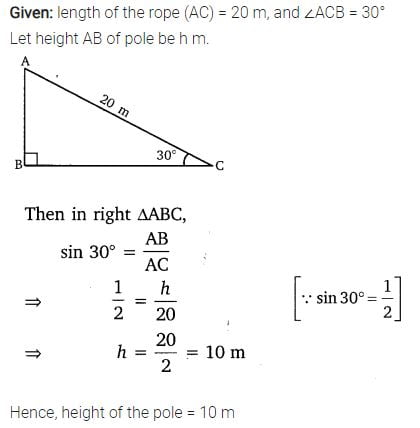
Class 10 Maths 9.1 NCERT Solutions Question 2.
2. A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Solution:
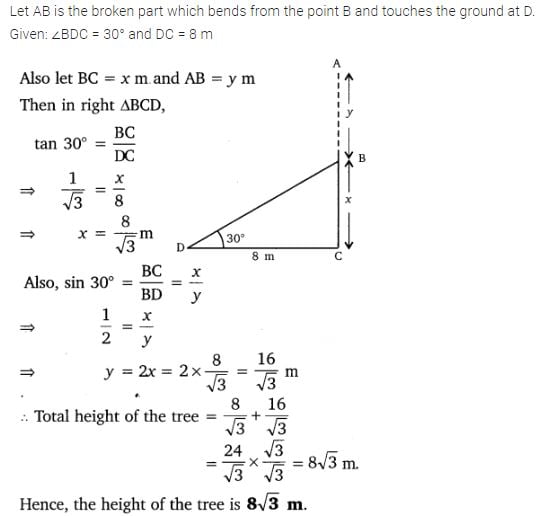
Class 10 Maths 9.1 NCERT Solutions Question 3.
3. A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Solution:

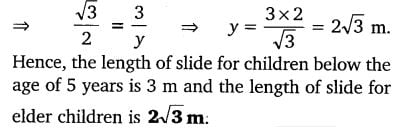
Class 10 Maths 9.1 NCERT Solutions Question 4.
4. The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Solution:

Class 10 Maths 9.1 NCERT Solutions Question 5.
5. A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Solution:
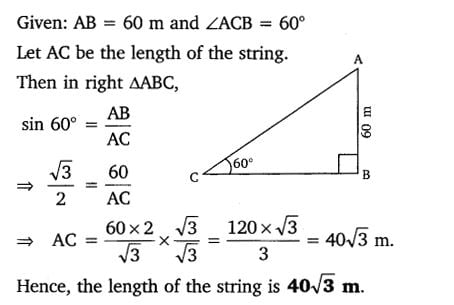
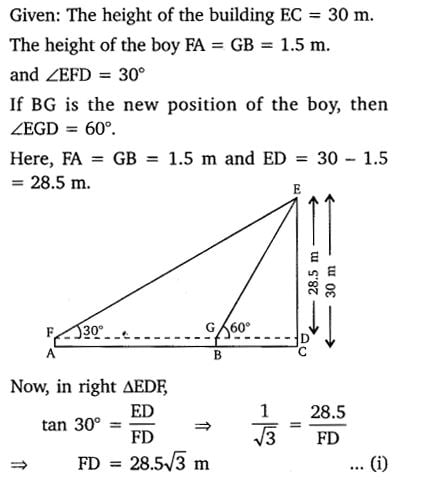
Class 10 Maths 9.1 NCERT Solutions Question 6.
6. A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the
building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Solution:

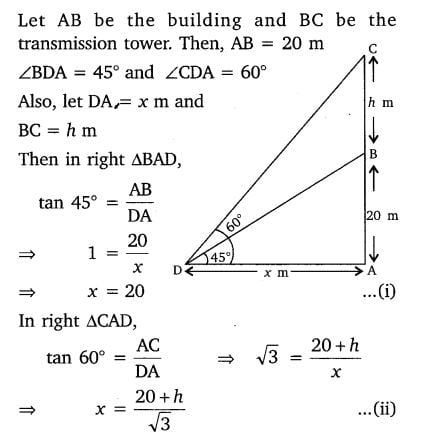
Class 10 Maths 9.1 NCERT Solutions Question 7.
7. From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Solution:

Class 10 Maths 9.1 NCERT Solutions Question 8.
8. A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Solution:

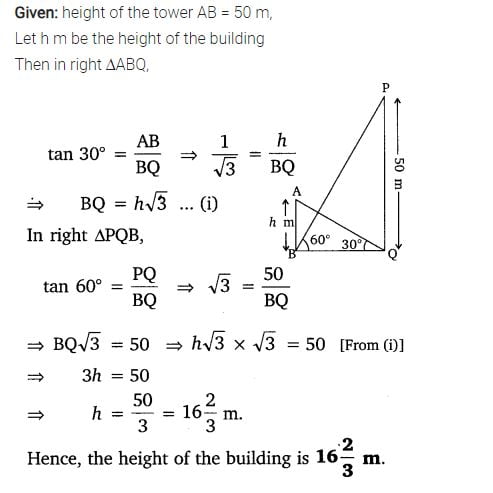
Class 10 Maths 9.1 NCERT Solutions Question 9.
9. The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Solution:
Class 10 Maths 9.1 NCERT Solutions Question 10.
10. Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.
Solution:


Class 10 Maths 9.1 NCERT Solutions Question 11.
11. A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see Fig. 9.12). Find the height of the tower and the width of the canal.

Solution:


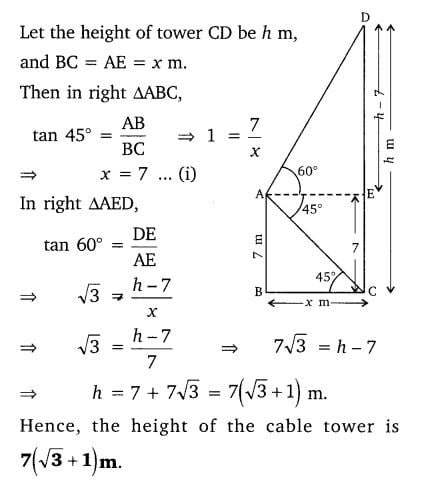
Class 10 Maths 9.1 NCERT Solutions Question 12.
12. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution:
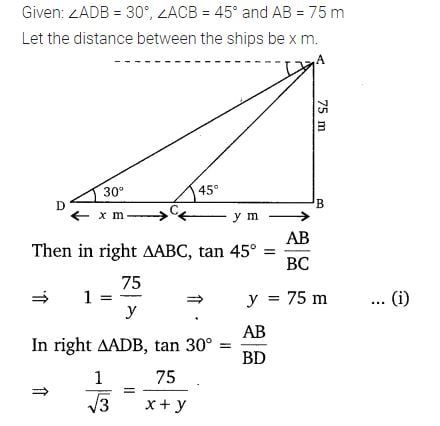
Class 10 Maths 9.1 NCERT Solutions Question 13.
13. As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Solution:

Class 10 Maths 9.1 NCERT Solutions Question 14.
14. A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see Fig. 9.13). Find the distance travelled by the balloon during the interval.

Solution:

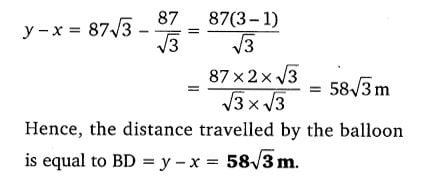
Class 10 Maths 9.1 NCERT Solutions Question 15.
15. A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution:

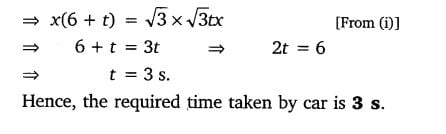
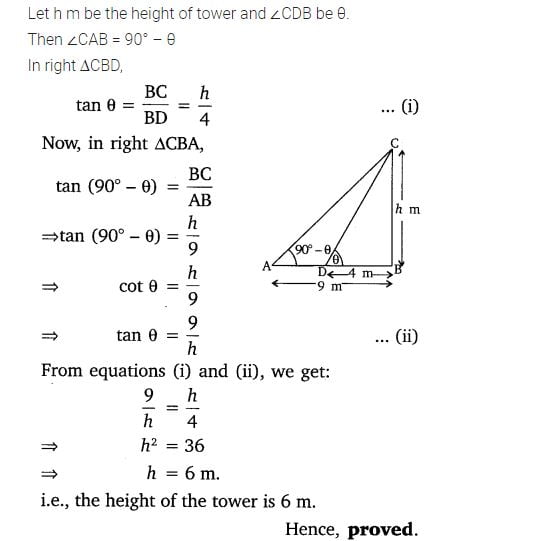
Class 10 Maths 9.1 NCERT Solutions Question 16.
16. The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Solution:
Maths in Class 10: Some Applications of Trigonometry
In Class 10 Maths 9.1 NCERT Solutions Students will talk about patterns in terms that come after those that come after by adding a certain number to the terms that came before in this chapter. Additionally, they see how to calculate the sum of n successive terms and the nth term. When students tackle real-world situations, they will successfully understand Some Applications of Trigonometry.
As a result, these NCERT Solutions for Class 10 Maths will aid students in comprehending various question formats and their responses, in addition to providing important shortcuts and diagrammatic explanations. The Class 10 Maths Chapter 9 PDF NCERT Solutions are all provided in easy-to-understand manner. Students who fully understand these solutions will be able to solve challenging situations with ease.
The teachers have carefully selected the Class 10 NCERT Solutions to help students become more adept at solving problems. Students can consult Bhautik study materials for Introduction To Trigonometry for a clearer understanding.
Every step of the solutions offered by Bhautik Study is discussed in great depth and with clarity. To help students better prepare for their board exams, subject matter experts have created the NCERT Class 10 Maths Solutions. These answers will be useful not only for studying for exams but also for completing assignments and homework.
The NCERT textbooks are frequently the source of questions on the CBSE Class 10 test, either directly or indirectly. Therefore, one of the greatest tools for getting ready and equipping oneself to tackle any kind of exam question from the chapter is the NCERT Solutions for Class 10 Maths Chapter 9 Some Application of Trigonometry.
What is the Advantage of Class 10 Maths NCERT Solutions Chapter 9 Provided by Bhautik Study?
Class 10 Maths 9.1 NCERT Solutions
Introduction to trigonometry is a fundamental topic in mathematics, particularly in geometry and calculus. In Class 10, students typically begin their journey into trigonometry by learning about the basic trigonometric functions, namely sine, cosine, and tangent, along with their reciprocal functions cosecant, secant, and cotangent.
Here’s a brief overview of what students usually cover in an introduction to trigonometry in Class 10:
Trigonometric Ratios: Students learn about the ratios of sides of a right-angled triangle with respect to its acute angles. These ratios are sine (sin), cosine (cos), and tangent (tan), defined as follows:
- Sin θ = Opposite Side/Hypotenuse
- Cos θ = Adjacent Side/Hypotenuse
- Tan θ = Opposite Side/Adjacent Side
Reciprocal Trigonometric Ratios: Along with sine, cosine, and tangent, students also learn about their reciprocal functions:
- Cosec θ = 1/Sin θ
- Sec θ = 1/Cos θ
- Cot θ = 1/Tan θ
Applications of Trigonometry: Students explore how trigonometry is applied in various real-life situations, such as calculating heights of buildings or distances between objects using angles of elevation and depression.
Trigonometric Identities: Although not extensively covered at this stage, students may be introduced to basic trigonometric identities like:
- Sin^2 θ + Cos^2 θ = 1
- Tan θ = Sin θ / Cos θ
Solving Right Triangles: Students learn to solve right triangles, where they are given certain information about the triangle and are tasked with finding the remaining sides or angles using trigonometric ratios.
Use of Trigonometric Tables: Though less common in the age of calculators and computers, students may still be introduced to trigonometric tables and how to use them to find trigonometric values.
Overall, the introduction to trigonometry in Class 10 lays the foundation for more advanced topics in trigonometry and calculus in higher classes. It’s a crucial step in understanding the relationships between angles and sides of triangles and their applications in solving real-world problems here Class 10 Maths 9.1 NCERT Solutions play an important role.