Table of Contents
ToggleClass 10 maths 8.3 NCERT solutions
NCERT Solutions For Class 10 Maths Chapter 8 Introduction to Trigonometry Ex-8.3
Download the free NCERT Maths Chapter 8 Solutions for Class 10 here Introduction to Trigonometry in Maths Class 10 NCERT Solutions are a great resource for homework assistance. For class 10 maths 8.3 NCERT solutions Expert Bhautikstudy.com Teachers developed the NCERT Solutions. Complete solutions to all the problems in NCERT Textbook’s Chapter 8 Math Class 10 Triangles Exercise 8.3.
Class 10 Maths 8.3 NCERT Solutions Question 1.
1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution:

Class 10 Maths 8.3 NCERT Solutions Question 2.
2. Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:

Class 10 Maths 8.3 NCERT Solutions Question 3.
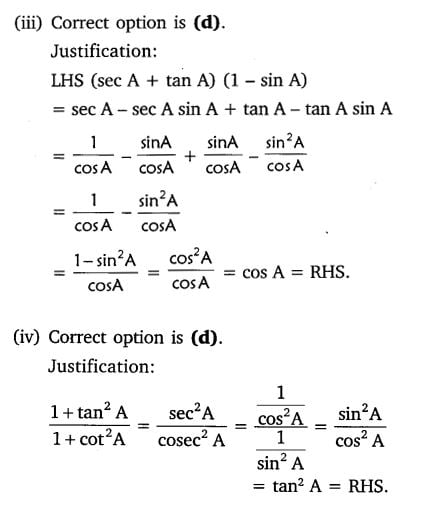
3. Choose the correct option. Justify your choice.
(i) 9 sec2A – 9 tan2A =
(A) 1 (B) 9 (C) 8 (D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
(A) 0 (B) 1 (C) 2 (D) – 1
(iii) (sec A + tan A) (1 – sin A) =
(A) sec A (B) sin A (C) cosec A (D) cos A
(iv) 1+tan2A/1+cot2A =
(A) sec2 A (B) -1 (C) cot2A (D) tan2A
Solution:

Class 10 Maths 8.3 NCERT Solutions Question 4.
4. Prove the following identities, where the angles involved are acute angles for which the
expressions are defined.
(i) (cosec θ – cot θ)2 = (1-cos θ)/(1+cos θ)
(ii) cos A/(1+sin A) + (1+sin A)/cos A = 2 sec A
(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ
[Hint : Write the expression in terms of sin θ and cos θ]
(iv) (1 + sec A)/sec A = sin2A/(1-cos A)
[Hint : Simplify LHS and RHS separately]
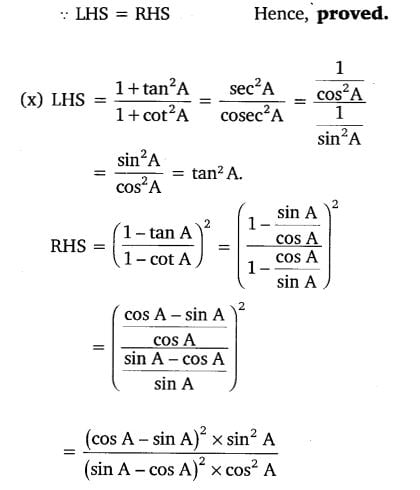
(v) ( cos A–sin A+1)/( cos A +sin A–1) = cosec A + cot A, using the identity cosec2A = 1+cot2A.
![]()
(vii) (sin θ – 2sin3θ)/(2cos3θ-cos θ) = tan θ
(viii) (sin A + cosec A)2 + (cos A + sec A)2 = 7+tan2A+cot2A

Solution:







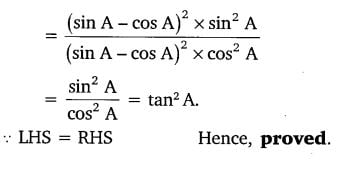
Maths in Class 10: Introduction to Trigonometry
In Class 10 Maths 8.3 NCERT Solutions Students will talk about patterns in terms that come after those that come after by adding a certain number to the terms that came before in this chapter. Additionally, they see how to calculate the sum of n successive terms and the nth term. When students tackle real-world situations, they will successfully understand Introduction to Trigonometry.
As a result, these NCERT Solutions for Class 10 Maths will aid students in comprehending various question formats and their responses, in addition to providing important shortcuts and diagrammatic explanations. The Class 10 Maths Chapter 8 PDF NCERT Solutions are all provided in easy-to-understand manner. Students who fully understand these solutions will be able to solve challenging situations with ease.
The teachers have carefully selected the Class 10 NCERT Solutions to help students become more adept at solving problems. Students can consult Bhautik study materials for Introduction To Trigonometry for a clearer understanding here Class 10 Maths 8.3 NCERT Solutions play an important role.
Every step of the solutions offered by Bhautik Study is discussed in great depth and with clarity. To help students better prepare for their board exams, subject matter experts have created the NCERT Class 10 Maths Solutions. These answers will be useful not only for studying for exams but also for completing assignments and homework.
The NCERT textbooks are frequently the source of questions on the CBSE Class 10 test, either directly or indirectly. Therefore, one of the greatest tools for getting ready and equipping oneself to tackle any kind of exam question from the chapter is the NCERT Solutions for Class 10 Maths Chapter 8 Introduction to trigonometry.
What is the Advantage of Class 10 Maths NCERT Solutions Chapter 8 Provided by Bhautik Study?
Class 10 Maths 8.3 NCERT Solutions
Introduction to trigonometry is a fundamental topic in mathematics, particularly in geometry and calculus. In Class 10, students typically begin their journey into trigonometry by learning about the basic trigonometric functions, namely sine, cosine, and tangent, along with their reciprocal functions cosecant, secant, and cotangent.
Here’s a brief overview of what students usually cover in an introduction to trigonometry in Class 10:
Trigonometric Ratios: Students learn about the ratios of sides of a right-angled triangle with respect to its acute angles. These ratios are sine (sin), cosine (cos), and tangent (tan), defined as follows:
- Sin θ = Opposite Side/Hypotenuse
- Cos θ = Adjacent Side/Hypotenuse
- Tan θ = Opposite Side/Adjacent Side
Reciprocal Trigonometric Ratios: Along with sine, cosine, and tangent, students also learn about their reciprocal functions:
- Cosec θ = 1/Sin θ
- Sec θ = 1/Cos θ
- Cot θ = 1/Tan θ
Applications of Trigonometry: Students explore how trigonometry is applied in various real-life situations, such as calculating heights of buildings or distances between objects using angles of elevation and depression.
Trigonometric Identities: Although not extensively covered at this stage, students may be introduced to basic trigonometric identities like:
- Sin^2 θ + Cos^2 θ = 1
- Tan θ = Sin θ / Cos θ
Solving Right Triangles: Students learn to solve right triangles, where they are given certain information about the triangle and are tasked with finding the remaining sides or angles using trigonometric ratios.
Use of Trigonometric Tables: Though less common in the age of calculators and computers, students may still be introduced to trigonometric tables and how to use them to find trigonometric values.
Overall, the introduction to trigonometry in Class 10 lays the foundation for more advanced topics in trigonometry and calculus in higher classes. It’s a crucial step in understanding the relationships between angles and sides of triangles and their applications in solving real-world problems here Class 10 Maths 8.3 NCERT Solutions play an important role.