Table of Contents
ToggleClass 10 maths 6.2 NCERT solutions
NCERT Solutions For Class 10 Maths Chapter 6 Triangles Ex-6.2
Download the free NCERT Maths Chapter 6 Solutions for Class 10 here Triangles in Maths Class 10 NCERT Solutions are a great resource for homework assistance. For class 10 maths 6.2 NCERT solutions Expert Bhautikstudy.com Teachers developed the NCERT Solutions. Complete solutions to all the problems in NCERT Textbook’s Chapter 6 Math Class 10 Triangles Exercise 6.2.
Class 10 Maths 6.2 NCERT Solutions Question 1.
1. In figure. (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).

Solution:

Class 10 Maths 6.2 NCERT Solutions Question 2.
2. E and F are points on the sides PQ and PR, respectively of a ΔPQR. For each of the following cases, state whether EF || QR.
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.63 cm
Solution:

Class 10 Maths 6.2 NCERT Solutions Question 3.
3. In the figure, if LM || CB and LN || CD, prove that AM/AB = AN/AD

Solution:

Class 10 Maths 6.2 NCERT Solutions Question 4.
4. In the figure, DE||AC and DF||AE. Prove that BF/FE = BE/EC

Solution:

Class 10 Maths 6.2 NCERT Solutions Question 5.
5. In the figure, DE||OQ and DF||OR, show that EF||QR.

Solution:

Class 10 Maths 6.2 NCERT Solutions Question 6.
6. In the figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Solution:

Class 10 Maths 6.2 NCERT Solutions Question 7.
7. Using Basic proportionality theorem, prove that a line drawn through the mid-points of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).

Solution:
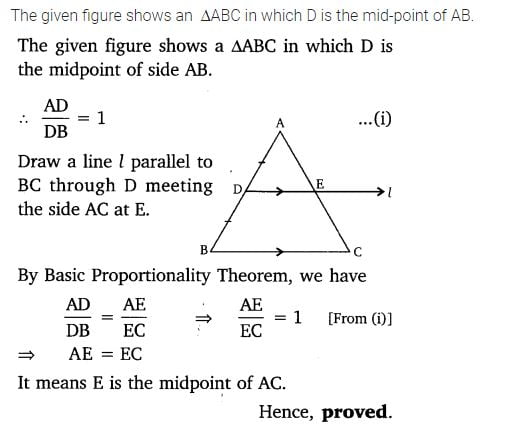
Class 10 Maths 6.2 NCERT Solutions Question 8.
8. Using Converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
Solution:
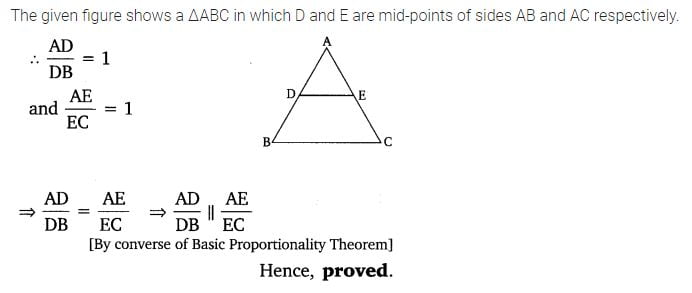
Class 10 Maths 6.2 NCERT Solutions Question 9.
9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that AO/BO = CO/DO.
Solution:
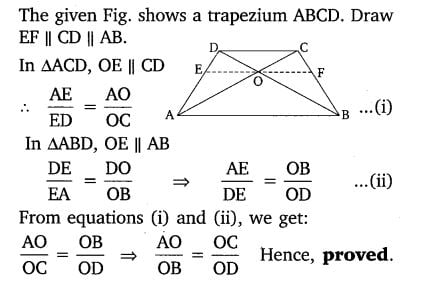
Class 10 Maths 6.2 NCERT Solutions Question 10.
10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that AO/BO = CO/DO. Show that ABCD is a trapezium.
Solution:
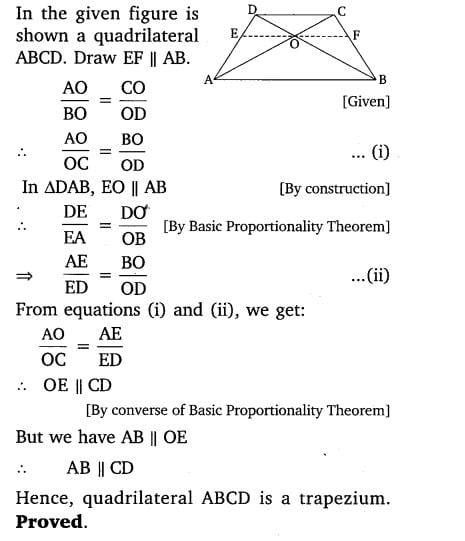
Maths in Class 10: Triangles
In Class 10 Maths 6.2 NCERT Solutions Students will talk about patterns in terms that come after those that come after by adding a certain number to the terms that came before in this chapter. Additionally, they see how to calculate the sum of n successive terms and the nth term. When students tackle real-world situations, they will successfully understand Triangles.
Basic Proportionality Theorem (BPT) and its Converse
Basic Proportionality Theorem
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then other two sides are divided in the same ratio. Thus in ∆ABC, if DE || BC, then![]()
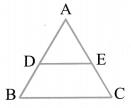
Converse of BPT
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side,
Every step of the solutions offered by Bhautik Study is discussed in great depth and with clarity. To help students better prepare for their board exams, subject matter experts have created the NCERT Class 10 Maths Solutions. These answers will be useful not only for studying for exams but also for completing assignments and homework.
The NCERT textbooks are frequently the source of questions on the CBSE Class 10 test, either directly or indirectly. Therefore, one of the greatest tools for getting ready and equipping oneself to tackle any kind of exam question from the chapter is the NCERT Solutions for Class 10 Maths Chapter 6 Triangles.
What is the Advantage of Class 10 Maths NCERT Solutions Chapter 6 Provided by Bhautik Study?
Class 10 Maths 6.2 NCERT Solutions
In mathematics, a triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. In class 10, students typically learn about various properties and concepts related to triangles. Here’s a brief overview of what is usually covered in Class 10 Maths 6.2 NCERT Solutions:
Types of Triangles:
- Equilateral Triangle: All three sides are of equal length, and all three angles are equal (each measuring 60 degrees).
- Isosceles Triangle: Two sides are of equal length, and consequently, two angles are equal.
- Scalene Triangle: No sides are of equal length, and no angles are equal.
Angles:
- Sum of Angles: The sum of the interior angles of a triangle is always 180 degrees.
- Exterior Angle: The exterior angle of a triangle is equal to the sum of the two opposite interior angles.
Properties:
- Side Lengths: The sum of the lengths of any two sides of a triangle is greater than the length of the third side (Triangle Inequality Theorem).
- Altitudes: Perpendiculars drawn from each vertex to the opposite side are called altitudes. The point where the altitude intersects the side is called the foot of the altitude.
- Medians: A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side.
- Angle Bisectors: An angle bisector of a triangle is a line segment that bisects one of the vertex angles of the triangle.
- Orthocenter: The point where all three altitudes of a triangle intersect.
- Centroid: The point where all three medians of a triangle intersect.
- Circumcenter: The point where the perpendicular bisectors of the sides of a triangle intersect.
Congruence and Similarity:
- Triangles are congruent if their corresponding sides and angles are equal.
- Triangles are similar if their corresponding angles are equal and their corresponding sides are in proportion.
Pythagoras Theorem:
- In a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Area of a Triangle:
- Various methods can be used to calculate the area of a triangle, including the formula: Area = (1/2) * base * height.
These are some fundamental concepts related to triangles that are typically covered in class 10 mathematics curriculum. Students often solve problems and apply these concepts to various geometric and real-world situations here Class 10 Maths 6.2 NCERT Solutions play an important role.