NCERT Solutions For Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2
Download the free NCERT Maths Chapter 5 Solutions for Class 10 here Arithmetic Progressions in Maths Class 10 NCERT Solutions are a great resource for homework assistance. For class 10 maths 5.2 ncert solutions Expert Bhautikstudy.com Teachers developed the NCERT Solutions. Complete solutions to all the problems in NCERT Textbook’s Chapter 5 Math Class 10 Pair of Linear Equations in Two Variables Exercise 5.2.
Class 10 Maths 5.2 NCERT Solutions Question 1.
1. Fill in the blanks in the following table, given that a is the first term, d the common difference and an the nth term of the A.P.
Solution:
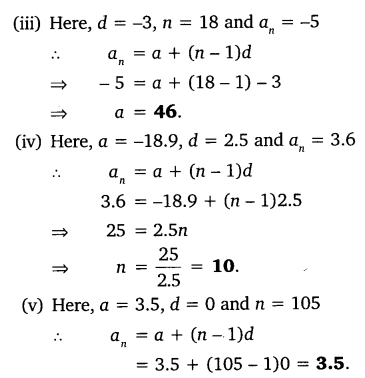
Class 10 Maths 5.2 NCERT Solutions Question 2.
2. Choose the correct choice in the following and justify:
Solution:
Class 10 Maths 5.2 NCERT Solutions Question 3.
3. In the following APs find the missing term in the boxes.
Solution:
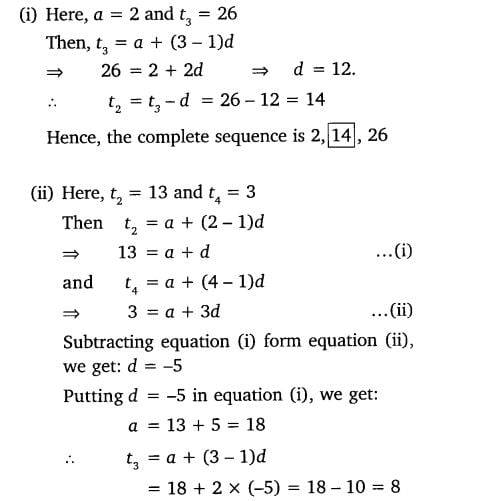
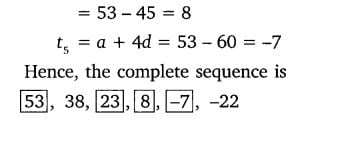
Class 10 Maths 5.2 NCERT Solutions Question 4.
4. Which term of the A.P. 3, 8, 13, 18, … is 78?
Solution:
Class 10 Maths 5.2 NCERT Solutions Question 5.
5. Find the number of terms in each of the following A.P.
(i) 7, 13, 19, …, 205
Solution:
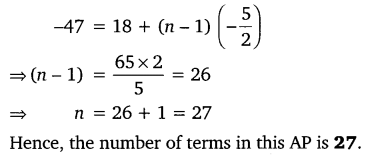
Class 10 Maths 5.2 NCERT Solutions Question 6.
6. Check whether -150 is a term of the A.P. 11, 8, 5, 2, …
Solution:
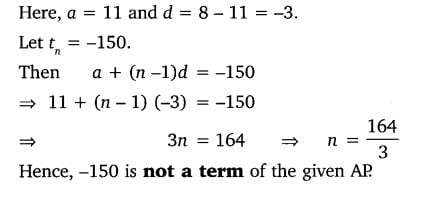
Class 10 Maths 5.2 NCERT Solutions Question 7.
7. Find the 31st term of an A.P. whose 11th term is 38 and the 16th term is 73.
Solution:
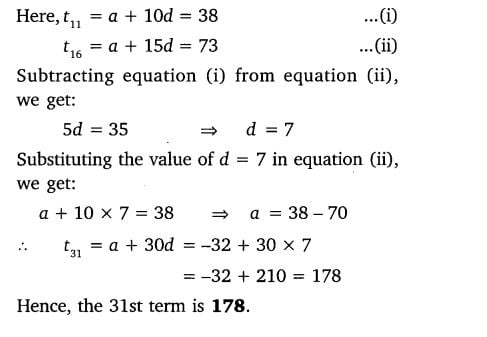
Class 10 Maths 5.2 NCERT Solutions Question 8.
8. An A.P. consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term.
Solution:
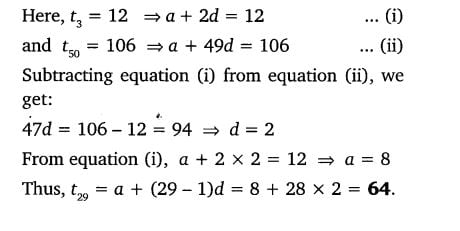
Class 10 Maths 5.2 NCERT Solutions Question 9.
9. If the 3rd and the 9th terms of an A.P. are 4 and − 8 respectively. Which term of this A.P. is zero.
Solution:
Class 10 Maths 5.2 NCERT Solutions Question 10.
10. If 17th term of an A.P. exceeds its 10th term by 7. Find the common difference.
Solution:
Class 10 Maths 5.2 NCERT Solutions Question 11.
11. Which term of the A.P. 3, 15, 27, 39,.. will be 132 more than its 54th term?
Solution:
Class 10 Maths 5.2 NCERT Solutions Question 12.
12. Two APs have the same common difference. The difference between their 100th term is 100, what is the difference between their 1000th terms?
Solution:
Class 10 Maths 5.2 NCERT Solutions Question 13.
13. How many three digit numbers are divisible by 7?
Solution:
Class 10 Maths 5.2 NCERT Solutions Question 14.
14. How many multiples of 4 lie between 10 and 250?
Solution:
Class 10 Maths 5.2 NCERT Solutions Question 15.
15. For what value of n, are the nth terms of two APs 63, 65, 67, and 3, 10, 17, … equal?
Solution:
Class 10 Maths 5.2 NCERT Solutions Question 16.
16. Determine the A.P. whose third term is 16 and the 7th term exceeds the 5th term by 12.
Solution:
Class 10 Maths 5.2 NCERT Solutions Question 17.
17. Find the 20th term from the last term of the A.P. 3, 8, 13, …, 253.
Solution:
Class 10 Maths 5.2 NCERT Solutions Question 18.
18. The sum of 4th and 8th terms of an A.P. is 24 and the sum of the 6th and 10th terms is 44. Find the first three terms of the A.P.
Solution:
Class 10 Maths 5.2 NCERT Solutions Question 19.
19. Subba Rao started work in 1995 at an annual salary of Rs 5000 and received an increment of Rs 200 each year. In which year did his income reach Rs 7000?
Solution:
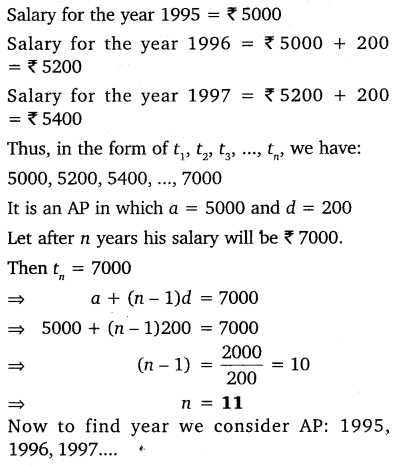
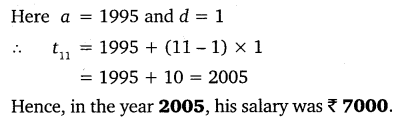
Class 10 Maths 5.2 NCERT Solutions Question 20.
20. Ramkali saved Rs 5 in the first week of a year and then increased her weekly saving by Rs 1.75. If in the nth week, her weekly savings become Rs 20.75, find n.
Solution:
Maths in Class 10: Arithmetic Progressions
In Class 10 Maths 5.2 NCERT Solutions Students will talk about patterns in terms that come after those that come after by adding a certain number to the terms that came before in this chapter. Additionally, they see how to calculate the sum of n successive terms and the nth term. When students tackle real-world situations, they will successfully understand arithmetic progression.
The nth term and the sum of the first n terms of an A.P. are derived using the Arithmetic Progression and applied to solve real-world situations in this chapter. From the perspective of the Class 10 exam, this is one of the most significant chapters. Since practically all competitive exams include questions on arithmetic progression, understanding an arithmetic progression is a fundamental and crucial subject to learn here Class 10 Maths 5.2 NCERT Solutions play an Important role.
The composition of the Quadratic Equations Class 10 Maths 5.2 NCERT Solutions has been designed to facilitate comprehension for all students. The knowledgeable staff at Bhautik Study has worked really hard to create an engaging and enjoyable Class 10 Maths 5.2 NCERT Solutions Chapter 5 Solutions. Without a question, maths is a difficult subject to learn. The formulas are difficult for pupils to learn, and they have difficulty using tactics when they should and here Class 10 Maths 5.2 NCERT Solutions play an important role.
Arithmatic Progressions in Chapter 5 of Maths Class 10 can be used to get the value of x. Aside from this, Class 10 Maths Chapter 5 provides about three methods for this. However, not everyone can easily understand all three of these approaches. Nevertheless, the Bhautik Study professionals have presented all three approaches in a very engaging manner that any student can readily understand in Chapter 5 Maths Class 10 NCERT Solutions. The explanations of all quadratic equation principles and formulas are clear. For the purpose of providing basic knowledge, the origin of the formula, its discovery process, the person who discovered it, and several other items are initially discussed.
Subsequently, NCERT Solution Class 10 Maths Chapter 5 provides numerous solved examples to help students learn how to use formulae and answer numerical problems. The Bhautik Study specialists have completed all of the NCERT exercises for the students. For the students’ practice, Class 10 Maths 5.2 NCERT Solutions NCERT Solutions also includes a few unanswered questions. In addition, the questions from the preceding year have been included in between the NCERT Solutions. It is also stated which question appeared in which year for the convenience of the pupils. For students’ better preparation, a few mock test papers are also included at the end of the PDF.
With complete assurance, we state that the NCERT Class 10 Maths 5.2 NCERT Solutions by Bhautik Study is the only thing you need to succeed in the board exams. Students only need to click on the link on the Bhautik Study website to obtain the free PDF.
What is the Advantage of Class 10 Maths NCERT Solutions Chapter 5 Provided by Bhautik Study?
Class 10 Maths 5.2 NCERT Solutions
Arithmetic Progressions (AP) are an essential topic in mathematics, commonly taught in Class 10 (in many educational systems). Here’s a concise overview of arithmetic progressions:
Definition:
An arithmetic progression (AP) is a sequence of numbers in which the difference between consecutive terms is constant. This constant difference is called the “common difference.”
General Form:
The general form of an arithmetic progression is:
Where:
- is the first term,
- is the common difference,
- is the number of terms in the sequence.
Properties:
- Common Difference (d): The difference between any two consecutive terms is constant.
- Nth Term (or General Term): The nth term of an AP is given by: .
- Sum of ‘n’ Terms (Arithmetic Series): The sum of the first terms of an AP, denoted by , is given by:
Examples of Arithmetic Progressions:
- , .
- , .
- , .
Finding Terms and Sums:
- Finding a Term: Given the first term , the common difference , and the position , we can find the th term using the formula: .
- Finding the Sum: To find the sum of the first terms , we use the formula mentioned above.
Solving Problems:
- Finding Unknown Terms: Given some terms of an AP, you may be asked to find the unknown terms or the common difference.
- Finding Sum: Sometimes, you may need to find the sum of a certain number of terms in the AP.
- Finding Position: You might also be asked to find the position of a certain term in the AP.
Applications:
Arithmetic progressions have numerous applications in real life, such as calculating financial progressions, analyzing patterns, and in various fields of science and engineering.
Understanding arithmetic progressions is crucial not only for Class 10 mathematics but also for higher-level mathematics and various applications in different fields here Class 10 Maths 5.2 NCERT Solutions play an important role.
